PROGRAM
11:00 (GMT+3)
 |
Xiaohua Zhu Peking University |
|
Bio: Xiaohua Zhu is a Professor at the Department of Mathematics at Peking University. He graduated from Hangzhou University in 1990 and received his PhD in 1995. Professor Zhu is mainly engaged in the research of differential geometry and geometric analysis. He has deep research work in complex geometry, Ricci flow, complex Monge-Ampere equation, Ricci solitons, ring-type algebraic cluster geometry, minimal small manifolds and so on. He has published over 50 papers in journals such as Acta Math., JAMS, Duke Math., GAFA, JEMS, etc. He was awarded the Outstanding Youth Prize by Hong Kong Qiushi Foundation in 2001, the Henry Fok Education Fund of the Ministry of Education of China in 2002, the National Natural Science Fund for Outstanding Youth in 2004, the ICTP Prize for young scientists in 2005, the Second Prize of the National Natural Science Award in 2014, and the 16th Shing S. Chern Mathematics Award in 2017. In 2009, he was elected Changjiang Distinguished Professor of the Ministry of Education of China. He is an invited speaker of ICM 2022 and the editorial board member of Acta Math. Sinica and Advances in Mathematics (China). |
|
Kaehler-Ricci flow on Fano G-manifolds.
I will talk about a recent work jointly with Tian on Kaehler-Ricci flow on Fano G-manifolds. We prove that on a Fano G-manifold, the Gromov-Hausdorff limit of Kaehler-Ricci flow with initial metric in $2\pi c_1(M)$ must be a Q-Fano horosymmetric variety which admits a singular Keahler-Ricci soliton. Moreover, we show that the complex structure of limit variety can be constructed by a $C^*$-degeneration induced by an element in the Cartan torus Lie algebra of G. A similar result can be also proved for Kaehler-Ricci flows on any Fano horosymmetric manifolds.
12:00 (GMT+3)
 |
Vladimir Bogachev Lomonosov Moscow State University |
|
Bio: Vladimir Bogachev is a professor at the Chair of Function Theory and Functional Analysis of Lomonosov Moscow State University, and also the Corresponding Member of the Russian Academy of Science. He graduated from the Faculty of Mechanics and Mathematics of Moscow State University in 1983 and has been working there since 1986. He obtained the degree of Doctor of Physical and Mathematical Sciences in 1991. Bogachev is the author of more than 200 papers in scientific journals and 15 monographs. His scientific interests include measure theory, probability theory, diffusion processes, stochastic analysis, nonlinear infinite-dimensional analysis, and Fokker-Planck-Kolmogorov equations. Vladimir Bogachev was awarded a prize from the Presidium of the USSR Academy of Sciences for young scientists (1990), a prize from the Japan Society for the Promotion of Science (2000), and the Kolmogorov prize of the Russian Academy of Sciences (2016). He is a member of the editorial boards of the journals “Analysis Mathematica”, “European Journal of Mathematics”, “Infinite-Dimensional Analysis, Quantum Probability and Related Topics”, “Theory of Probability and Its Applications”, “Izvestia Mathematics”, “Functional Analysis and Its Applications”, “Moscow Mathematical Journal”. |
|
Regularity of solutions to stationary Fokker-Planck-Kolmogorov equations.
We discuss the regularity of solutions to double divergence form equations of the form
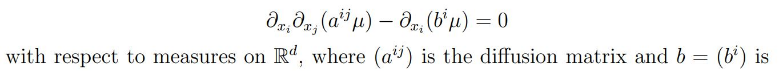
the drift coefficient. The equation is understood in the sense of distributions, so the coefficients can be rather irregular. The key problems concern the existence of solution densities and their regularity properties, and also the existence and uniqueness of probability solutions. In particular, we discuss some recent results obtained jointly with Röckner and Shaposhnikov on Zvonkin’s transform of the drift coefficient, which enables one to improve the drift.
The meeting will be held in the form of a webinar on the Zoom platform.
Pre-registration for the event is not required.
Link to the conference:
https://us02web.zoom.us/j/83379698154?pwd=YTUzRG5RSUUxQzMybWNCTTNlZCtpQT09
Meeting ID : 833 7969 8154
Passcode:987654

