ПРОГРАММА
11:00 (МСК)
 |
Сяохуа Чжу Пекинский университет |
|
Биография: Сяохуа Чжу — профессор кафедры математики Пекинского университета. Он окончил Университет Ханчжоу в 1990 году и получил степень доктора философии в 1995 году. Профессор Чжу в основном занимается исследованиями в области дифференциальной геометрии и геометрического анализа. Он имеет глубокую исследовательскую работу в области комплексной геометрии, потока Риччи, комплексного уравнения Монжа-Ампера, солитонов Риччи, кольцевой алгебраической кластерной геометрии, минимальных малых многообразий и так далее. Он опубликовал более 50 статей в таких журналах, как Acta Math., JAMS, Duke Math., GAFA, JEMS и т. д. Он был награжден премией за выдающиеся достижения среди молодежи Гонконгского фонда Цюши в 2001 г., Образовательным фондом Генри Фока Министерства образования Китая в 2002 г., Национальным фондом естественных наук для выдающейся молодежи в 2004 г., премией ICTP для молодых ученых в 2005 г., второй Национальной премией в области естественных наук в 2014 г. и 16-й математической премией Черня в 2017 г. В 2009 году он был избран заслуженным профессором Чанцзяна Министерства образования Китая. Он приглашенный спикер ICM 2022 и член редакционной коллегии Acta Math. Sinica and Advances in Mathematics (Китай). |
|
Поток Кэлера-Риччи на G-многообразиях Фано.
I will talk about a recent work jointly with Tian on Kaehler-Ricci flow on Fano G-manifolds. We prove that on a Fano G-manifold, the Gromov-Hausdorff limit of Kaehler-Ricci flow with initial metric in $2\pi c_1(M)$ must be a Q-Fano horosymmetric variety which admits a singular Keahler-Ricci soliton. Moreover, we show that the complex structure of limit variety can be constructed by a $C^*$-degeneration induced by an element in the Cartan torus Lie algebra of G. A similar result can be also proved for Kaehler-Ricci flows on any Fano horosymmetric manifolds.
12:00 (МСК)
 |
Владимир Богачёв МГУ имени М.В. Ломоносова |
|
Биография: Владимир Богачев - профессор кафедры теории функций и функционального анализа Московского государственного университета имени М.В. Ломоносова, а также член-корреспондент Российской академии наук. Он окончил механико-математический факультет Московского государственного университета в 1983 году и работает там с 1986 года. В 1991 году он получил степень доктора физико-математических наук. Богачев является автором более 200 статей в научных журналах и 15 монографий. Его научные интересы включают теорию меры, теорию вероятностей, диффузионные процессы, стохастический анализ, нелинейный бесконечномерный анализ и уравнения Фоккера-Планка-Колмогорова. Владимир Богачев был удостоен премии Президиума Академии наук СССР для молодых ученых (1990), премии Японского общества содействия развитию науки (2000) и премии имени Колмогорова Российской академии наук (2016). Он является членом редколлегий журналов “Analysis Mathematica”, “European Journal of Mathematics”, “Бесконечномерный анализ, квантовая вероятность и смежные темы”, “Теория вероятностей и ее приложения”, “Известия математики”, “Функциональный анализ и его приложения”, “Московский Математический журнал”. |
|
Регулярность решений стационарных уравнений Фоккера-Планка-Колмогорова.
We discuss the regularity of solutions to double divergence form equations of the form
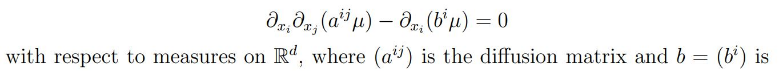
the drift coefficient. The equation is understood in the sense of distributions, so the coefficients can be rather irregular. The key problems concern the existence of solution densities and their regularity properties, and also the existence and uniqueness of probability solutions. In particular, we discuss some recent results obtained jointly with Röckner and Shaposhnikov on Zvonkin’s transform of the drift coefficient, which enables one to improve the drift.
Заседание пройдет в форме вебинара на платформе Zoom.
Предварительная регистрация на мероприятие не требуется.
Ссылка на конференцию:
https://us02web.zoom.us/j/83379698154?pwd=YTUzRG5RSUUxQzMybWNCTTNlZCtpQT09
Meeting ID : 833 7969 8154
Пароль:987654

